Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop. Given a statement regarding the category C, by interchanging the source and target of each morphism as well as interchanging the order of composing two morphisms, a corresponding dual statement is obtained regarding the opposite category Cop. Duality, as such, is the assertion that truth is invariant under this operation on statements. In other words, if a statement is true about C, then its dual statement is true about Cop. Also, if a statement is false about C, then its dual has to be false about Cop.
Given a concrete category C, it is often the case that the opposite category Cop per se is abstract. Cop need not be a category that arises from mathematical practice. In this case, another category D is also termed to be in duality with C if D and Cop are equivalent as categories.
In the case when C and its opposite Cop are equivalent, such a category is self-dual.
Contents |
Formal definition
We define the elementary language of category theory as the two-sorted first order language with objects and morphisms as distinct sorts, together with the relations of an object being the source or target of a morphism and a symbol for composing two morphisms.
Let σ be any statement in this language. We form the dual σop as follows:
- Interchange each occurrence of "source" in σ with "target".
- Interchange the order of composing morphisms. That is, replace each occurrence of
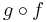 with
with 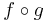
Informally, these conditions state that the dual of a statement is formed by reversing arrows and compositions.
Duality is the observation that σ is true for some category C if and only if σop is true for Cop.
Examples
- A morphism
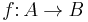 is a monomorphism if
is a monomorphism if 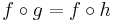 implies
implies 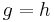 . Performing the dual operation, we get the statement that
. Performing the dual operation, we get the statement that 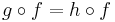 implies
implies 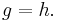 for a morphism
for a morphism 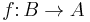 . This is precisely what it means for f to be an epimorphism. In short, the property of being a monomorphism is dual to the property of being an epimorphism.
. This is precisely what it means for f to be an epimorphism. In short, the property of being a monomorphism is dual to the property of being an epimorphism.
Applying duality, this means that a morphism in some category C is a monomorphism if and only if the reverse morphism in the opposite category Cop is an epimorphism.
- An example comes from reversing the direction of inequalities in a partial order. So if X is a set and ≤ a partial order relation, we can define a new partial order relation ≤new by
-
- x ≤new y if and only if y ≤ x.
This example on orders is a special case, since partial orders correspond to a certain kind of category in which Hom(A,B) can have at most one element. In applications to logic, this then looks like a very general description of negation (that is, proofs run in the opposite direction). For example, if we take the opposite of a lattice, we will find that meets and joins have their roles interchanged. This is an abstract form of De Morgan's laws, or of duality applied to lattices.
- Fibrations and cofibrations are examples of dual notions in algebraic topology and homotopy theory. In this context, the duality is often called Eckmann–Hilton duality.